Depth determination problem
off-line minimum problem
Problems 21-1: Off-line minimum(Page 517 of CLRS)
The off-line minimum problem asks us to maintain a dynamic set 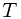 of elements from the domain
of elements from the domain ![\[\{1,2,\ldots,n\}\] \[\{1,2,\ldots,n\}\]](/user_files/llhuii/epics/a0209f91b2025ea4de1f74305c24201a8a3d13ef.png) under the operations INSERT and EXTRACT-MIN. We are given a sequence S of n INSERT and m EXTRACT-MIN calls, where each key in
under the operations INSERT and EXTRACT-MIN. We are given a sequence S of n INSERT and m EXTRACT-MIN calls, where each key in ![\[\{1,2,\ldots,n\}\] \[\{1,2,\ldots,n\}\]](/user_files/llhuii/epics/a0209f91b2025ea4de1f74305c24201a8a3d13ef.png) is inserted exactly once. We wish to determine which key is returned by each EXTRACT-MIN call. Specifically, we wish to fill in an array
is inserted exactly once. We wish to determine which key is returned by each EXTRACT-MIN call. Specifically, we wish to fill in an array ![\[extracted[1\ldots\,m]\] \[extracted[1\ldots\,m]\]](/user_files/llhuii/epics/fd2b0a6d6372bc89ea3b74e306e866771a0b786b.png) , where for
, where for ![\[i=1,2,\ldots,m\] \[i=1,2,\twodots,m\]](/user_files/llhuii/epics/667b3cdfd2a3217c1194cc352af03bb3b684bb9b.png)
![$,extracted[i]$ $,extracted[i]$](/user_files/llhuii/epics/87d8cb9ae79c87507e651386fbefa7b5b7969b62.png) is the key returned by the
is the key returned by the 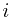 th EXTRACT-MIN call. The problem is "off-line" in the sense that we are allowed to process the entire sequence
th EXTRACT-MIN call. The problem is "off-line" in the sense that we are allowed to process the entire sequence 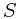 before determining any of the returned keys.
before determining any of the returned keys.
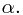 In the following instance of the off-line minimum problem, each INSERT is represented by a number and each EXTRACT-MIN is represented by the letter
In the following instance of the off-line minimum problem, each INSERT is represented by a number and each EXTRACT-MIN is represented by the letter 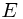 :
:
![\[4, 8, E, 3, E, 9, 2, 6, E, E, E, 1, 7, E, 5.\] \[4, 8, E, 3, E, 9, 2, 6, E, E, E, 1, 7, E, 5.\]](/user_files/llhuii/epics/58af8a945c77533ab78de2d41eb60485a2727f53.png)
Fill in the correct values in the extracted array.
To develop an algorithm for this problem, we break the sequence 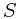 into homogeneous subsequences. That is, we represent
into homogeneous subsequences. That is, we represent 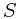 by
by
![\[I_{1},E,I_{2},E,I_{3},\ldots,I_{m},E,I_{m+1}\] \[I_{1},E,I_{2},E,I_{3},\ldots,I_{m},E,I_{m+1}\]](/user_files/llhuii/epics/96d1731291c07c36614dbd71f8bfdc4ff14f05d4.png)
where each 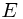 represents a single EXTRACT-MIN call and each
represents a single EXTRACT-MIN call and each 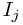 represents a (possibly empty) sequence of INSERT calls. For each subsequence
represents a (possibly empty) sequence of INSERT calls. For each subsequence 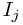 , we initially place the keys inserted by these operations into a set
, we initially place the keys inserted by these operations into a set 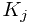 , which is empty if
, which is empty if 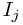 is empty. We then do the following.
is empty. We then do the following.

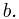 Argue that the array
Argue that the array 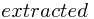 returned by OFF-LINE-MINIMUM is correct.
returned by OFF-LINE-MINIMUM is correct.
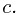 Describe how to implement OFF-LINE-MINIMUM efficiently with a disjoint-set data structure. Give a tight bound on the worst-case running time of your implementation.
Describe how to implement OFF-LINE-MINIMUM efficiently with a disjoint-set data structure. Give a tight bound on the worst-case running time of your implementation.
a) the 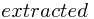 array will hold
array will hold 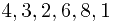 .
.
b)We will show that the extracted array is correct by contradiction. Assume that the extracted array is not correct. Let 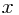 =
= ![$extracted[j]$ $extracted[j]$](/user_files/llhuii/epics/046666f107e74fa69e44c27c3236c8c25d4e0479.png) be the smallest value
be the smallest value ![$extracted[j]$ $extracted[j]$](/user_files/llhuii/epics/046666f107e74fa69e44c27c3236c8c25d4e0479.png) for which the extracted array is incorrect. Let the correct solution reside in the array correct. Call
for which the extracted array is incorrect. Let the correct solution reside in the array correct. Call 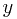 the value of
the value of ![$correct[j]$ $correct[j]$](/user_files/llhuii/epics/228882592fff409ff428e4a66a8cd7789fd1323c.png) . We have two cases, one where
. We have two cases, one where  and one where
and one where  We will prove that neither case can occur.
We will prove that neither case can occur.
Assume that  . Then the element
. Then the element 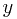 can’t appear in the extracted array, or it would have been the smallest value for which the extracted array was incorrect.Since we’ve already processed
can’t appear in the extracted array, or it would have been the smallest value for which the extracted array was incorrect.Since we’ve already processed 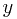 before processing
before processing 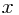 , it must have had a set value of
, it must have had a set value of  . But, if
. But, if ![$correct[j]$ $correct[j]$](/user_files/llhuii/epics/228882592fff409ff428e4a66a8cd7789fd1323c.png) was set to
was set to 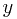 , then
, then 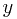 must initially have been in some
must initially have been in some 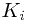 with
with 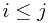 . Since
. Since ![$extracted[j]$ $extracted[j]$](/user_files/llhuii/epics/046666f107e74fa69e44c27c3236c8c25d4e0479.png) had no value yet when we processed
had no value yet when we processed 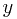 , then we couldn’t have put
, then we couldn’t have put 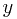 in set
in set 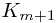 since we only union with the set above us and we haven’t unioned
since we only union with the set above us and we haven’t unioned 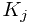 yet. Therefore, we can’t have
yet. Therefore, we can’t have  .
.
Assume that  . We argue that the element
. We argue that the element 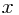 must appear in the correct array. Obviously
must appear in the correct array. Obviously 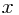 must appear before the
must appear before the 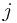 th extraction in the original sequence since the OFF-LINE-MINIMUM algorithm never moves sets of elements backwards, it only unions with sets later than it. If we hadn’t extracted
th extraction in the original sequence since the OFF-LINE-MINIMUM algorithm never moves sets of elements backwards, it only unions with sets later than it. If we hadn’t extracted 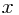 by the
by the 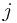 th extraction,then the optimal solutions should have chosen
th extraction,then the optimal solutions should have chosen 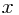 instead of
instead of 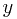 for the
for the 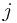 th extraction since
th extraction since 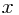 is smaller. Therefore, the optimal solution must have extracted
is smaller. Therefore, the optimal solution must have extracted 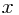 for some
for some  . But, that means that
. But, that means that ![$extracted[i]$ $extracted[i]$](/user_files/llhuii/epics/757e91aa0be6de9b8032560a69baa24220050ec7.png) holds some
holds some  . By similar reasoning as above, we couldn’t have moved
. By similar reasoning as above, we couldn’t have moved 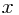 past set
past set 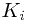 since
since ![$extracted[i]$ $extracted[i]$](/user_files/llhuii/epics/757e91aa0be6de9b8032560a69baa24220050ec7.png) would have been empty at the time
would have been empty at the time 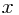 was chosen. So, since we only union with sets above us and
was chosen. So, since we only union with sets above us and 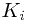 hasn’t been unioned yet, we can’t put
hasn’t been unioned yet, we can’t put 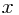 in
in ![$extracted[j]$ $extracted[j]$](/user_files/llhuii/epics/046666f107e74fa69e44c27c3236c8c25d4e0479.png) before
before ![$extracted[i]$ $extracted[i]$](/user_files/llhuii/epics/757e91aa0be6de9b8032560a69baa24220050ec7.png) . Therefore, we can’t have
. Therefore, we can’t have  .
.
Since we have shown that we must have ![$extracted[j]$ $extracted[j]$](/user_files/llhuii/epics/046666f107e74fa69e44c27c3236c8c25d4e0479.png) =
= ![$correct[j]$ $correct[j]$](/user_files/llhuii/epics/228882592fff409ff428e4a66a8cd7789fd1323c.png) for all
for all 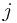 , the OFF-LINE-MINIMUM algorithm returns the correct array.
, the OFF-LINE-MINIMUM algorithm returns the correct array.
c)We can efficiently implement OFF-LINE-MINIMUM using a disjoint-set forest. We begin by creating 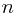 sets, one for each number, using the MAKE-SET operation. Then, we call UNION
sets, one for each number, using the MAKE-SET operation. Then, we call UNION  times to create the
times to create the 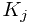 sets, the sequences of insertions between extractions. For each set
sets, the sequences of insertions between extractions. For each set 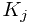 , we will also maintain 3 additional pieces of information, number, prev, and next in the representative element of the set (actually this information will be at all the elements, but it will only be maintained for the representative). number will correspond to
, we will also maintain 3 additional pieces of information, number, prev, and next in the representative element of the set (actually this information will be at all the elements, but it will only be maintained for the representative). number will correspond to 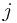 and can easily be set with the initial creating of the sets. prev will point to the representative element of
and can easily be set with the initial creating of the sets. prev will point to the representative element of 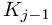 and next will point to the representative element of
and next will point to the representative element of 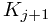 . We can maintain these three properties through unions as follows: when we union two sets
. We can maintain these three properties through unions as follows: when we union two sets 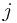 and
and 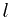 where
where 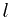 is the next set that still exists after
is the next set that still exists after 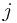 , we set number of the new representative equal to the maximum of the two representative numbers, in this case,
, we set number of the new representative equal to the maximum of the two representative numbers, in this case,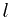 . We set prev of the new set equal to prev of set
. We set prev of the new set equal to prev of set 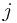 and we set next of prev of
and we set next of prev of 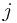 equal to the new representative element. Similarly, we set next of the new set equal to next of set
equal to the new representative element. Similarly, we set next of the new set equal to next of set 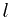 and we set prev of next of
and we set prev of next of 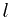 equal to the new representative element.
equal to the new representative element.
In the OFF-LINE-MINIMUM algorithm, each iteration of the for loop (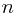 iterations) will first call FIND-SET on
iterations) will first call FIND-SET on 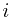 (line 2). We use the number field of the returned representative as
(line 2). We use the number field of the returned representative as 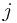 . Then, in line 5, to determine the smallest
. Then, in line 5, to determine the smallest 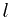 greater than
greater than 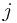 for which set
for which set 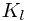 exists, we can simply follow the next pointer from
exists, we can simply follow the next pointer from 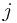 , which takes constant time. In line 6, we call UNION again, at most
, which takes constant time. In line 6, we call UNION again, at most 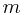 times throughout the
times throughout the 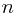 iterations. For each UNION call, we follow the procedure above for updating the number, prev and next, all of which take constant time. Therefore, we have a total of
iterations. For each UNION call, we follow the procedure above for updating the number, prev and next, all of which take constant time. Therefore, we have a total of 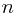 MAKE-SET operations,
MAKE-SET operations, 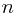 FIND-SET operations, and
FIND-SET operations, and 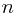 UNION operations. Since we have
UNION operations. Since we have 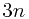 total operations and
total operations and 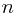 MAKE-SET operations, we know that the worst-case running time is
MAKE-SET operations, we know that the worst-case running time is 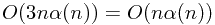 .
.
