off-line minimum problem
Problems 21-1: Off-line minimum(Page 517 of CLRS)
The off-line minimum problem asks us to maintain a dynamic set 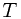 of elements from the domain
of elements from the domain ![\[\{1,2,\ldots,n\}\] \[\{1,2,\ldots,n\}\]](/user_files/llhuii/epics/a0209f91b2025ea4de1f74305c24201a8a3d13ef.png) under the operations INSERT and EXTRACT-MIN. We are given a sequence S of n INSERT and m EXTRACT-MIN calls, where each key in
under the operations INSERT and EXTRACT-MIN. We are given a sequence S of n INSERT and m EXTRACT-MIN calls, where each key in ![\[\{1,2,\ldots,n\}\] \[\{1,2,\ldots,n\}\]](/user_files/llhuii/epics/a0209f91b2025ea4de1f74305c24201a8a3d13ef.png) is inserted exactly once. We wish to determine which key is returned by each EXTRACT-MIN call. Specifically, we wish to fill in an array
is inserted exactly once. We wish to determine which key is returned by each EXTRACT-MIN call. Specifically, we wish to fill in an array ![\[extracted[1\ldots\,m]\] \[extracted[1\ldots\,m]\]](/user_files/llhuii/epics/fd2b0a6d6372bc89ea3b74e306e866771a0b786b.png) , where for
, where for ![\[i=1,2,\ldots,m\] \[i=1,2,\twodots,m\]](/user_files/llhuii/epics/667b3cdfd2a3217c1194cc352af03bb3b684bb9b.png)
![$,extracted[i]$ $,extracted[i]$](/user_files/llhuii/epics/87d8cb9ae79c87507e651386fbefa7b5b7969b62.png) is the key returned by the
is the key returned by the 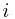 th EXTRACT-MIN call. The problem is "off-line" in the sense that we are allowed to process the entire sequence
th EXTRACT-MIN call. The problem is "off-line" in the sense that we are allowed to process the entire sequence 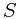 before determining any of the returned keys.
before determining any of the returned keys.
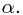 In the following instance of the off-line minimum problem, each INSERT is represented by a number and each EXTRACT-MIN is represented by the letter
In the following instance of the off-line minimum problem, each INSERT is represented by a number and each EXTRACT-MIN is represented by the letter 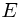 :
:
![\[4, 8, E, 3, E, 9, 2, 6, E, E, E, 1, 7, E, 5.\] \[4, 8, E, 3, E, 9, 2, 6, E, E, E, 1, 7, E, 5.\]](/user_files/llhuii/epics/58af8a945c77533ab78de2d41eb60485a2727f53.png)
Fill in the correct values in the extracted array.
To develop an algorithm for this problem, we break the sequence 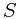 into homogeneous subsequences. That is, we represent
into homogeneous subsequences. That is, we represent 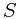 by
by
![\[I_{1},E,I_{2},E,I_{3},\ldots,I_{m},E,I_{m+1}\] \[I_{1},E,I_{2},E,I_{3},\ldots,I_{m},E,I_{m+1}\]](/user_files/llhuii/epics/96d1731291c07c36614dbd71f8bfdc4ff14f05d4.png)
where each 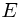 represents a single EXTRACT-MIN call and each
represents a single EXTRACT-MIN call and each 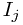 represents a (possibly empty) sequence of INSERT calls. For each subsequence
represents a (possibly empty) sequence of INSERT calls. For each subsequence 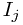 , we initially place the keys inserted by these operations into a set
, we initially place the keys inserted by these operations into a set 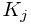 , which is empty if
, which is empty if 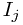 is empty. We then do the following.
is empty. We then do the following.

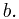 Argue that the array
Argue that the array 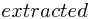 returned by OFF-LINE-MINIMUM is correct.
returned by OFF-LINE-MINIMUM is correct.
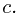 Describe how to implement OFF-LINE-MINIMUM efficiently with a disjoint-set data structure. Give a tight bound on the worst-case running time of your implementation.
Describe how to implement OFF-LINE-MINIMUM efficiently with a disjoint-set data structure. Give a tight bound on the worst-case running time of your implementation.
a) the 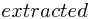 array will hold
array will hold 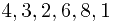 .
.
b)We will show that the extracted array is correct by contradiction. Assume that the extracted array is not correct. Let 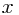 =
= ![$extracted[j]$ $extracted[j]$](/user_files/llhuii/epics/046666f107e74fa69e44c27c3236c8c25d4e0479.png) be the smallest value
be the smallest value ![$extracted[j]$ $extracted[j]$](/user_files/llhuii/epics/046666f107e74fa69e44c27c3236c8c25d4e0479.png) for which the extracted array is incorrect. Let the correct solution reside in the array correct. Call
for which the extracted array is incorrect. Let the correct solution reside in the array correct. Call 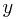 the value of
the value of ![$correct[j]$ $correct[j]$](/user_files/llhuii/epics/228882592fff409ff428e4a66a8cd7789fd1323c.png) . We have two cases, one where
. We have two cases, one where  and one where
and one where  We will prove that neither case can occur.
We will prove that neither case can occur.
Assume that  . Then the element
. Then the element 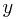 can’t appear in the extracted array, or it would have been the smallest value for which the extracted array was incorrect.Since we’ve already processed
can’t appear in the extracted array, or it would have been the smallest value for which the extracted array was incorrect.Since we’ve already processed 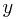 before processing
before processing 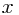 , it must have had a set value of
, it must have had a set value of  . But, if
. But, if ![$correct[j]$ $correct[j]$](/user_files/llhuii/epics/228882592fff409ff428e4a66a8cd7789fd1323c.png) was set to
was set to 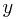 , then
, then 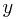 must initially have been in some
must initially have been in some 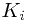 with
with 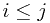 . Since
. Since ![$extracted[j]$ $extracted[j]$](/user_files/llhuii/epics/046666f107e74fa69e44c27c3236c8c25d4e0479.png) had no value yet when we processed
had no value yet when we processed 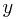 , then we couldn’t have put
, then we couldn’t have put 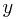 in set
in set 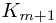 since we only union with the set above us and we haven’t unioned
since we only union with the set above us and we haven’t unioned 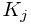 yet. Therefore, we can’t have
yet. Therefore, we can’t have  .
.
Assume that  . We argue that the element
. We argue that the element 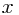 must appear in the correct array. Obviously
must appear in the correct array. Obviously 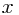 must appear before the
must appear before the 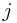 th extraction in the original sequence since the OFF-LINE-MINIMUM algorithm never moves sets of elements backwards, it only unions with sets later than it. If we hadn’t extracted
th extraction in the original sequence since the OFF-LINE-MINIMUM algorithm never moves sets of elements backwards, it only unions with sets later than it. If we hadn’t extracted 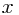 by the
by the 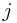 th extraction,then the optimal solutions should have chosen
th extraction,then the optimal solutions should have chosen 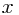 instead of
instead of 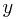 for the
for the 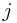 th extraction since
th extraction since 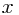 is smaller. Therefore, the optimal solution must have extracted
is smaller. Therefore, the optimal solution must have extracted 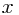 for some
for some  . But, that means that
. But, that means that ![$extracted[i]$ $extracted[i]$](/user_files/llhuii/epics/757e91aa0be6de9b8032560a69baa24220050ec7.png) holds some
holds some  . By similar reasoning as above, we couldn’t have moved
. By similar reasoning as above, we couldn’t have moved 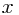 past set
past set 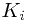 since
since ![$extracted[i]$ $extracted[i]$](/user_files/llhuii/epics/757e91aa0be6de9b8032560a69baa24220050ec7.png) would have been empty at the time
would have been empty at the time 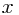 was chosen. So, since we only union with sets above us and
was chosen. So, since we only union with sets above us and 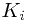 hasn’t been unioned yet, we can’t put
hasn’t been unioned yet, we can’t put 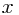 in
in ![$extracted[j]$ $extracted[j]$](/user_files/llhuii/epics/046666f107e74fa69e44c27c3236c8c25d4e0479.png) before
before ![$extracted[i]$ $extracted[i]$](/user_files/llhuii/epics/757e91aa0be6de9b8032560a69baa24220050ec7.png) . Therefore, we can’t have
. Therefore, we can’t have  .
.
Since we have shown that we must have ![$extracted[j]$ $extracted[j]$](/user_files/llhuii/epics/046666f107e74fa69e44c27c3236c8c25d4e0479.png) =
= ![$correct[j]$ $correct[j]$](/user_files/llhuii/epics/228882592fff409ff428e4a66a8cd7789fd1323c.png) for all
for all 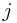 , the OFF-LINE-MINIMUM algorithm returns the correct array.
, the OFF-LINE-MINIMUM algorithm returns the correct array.
c)We can efficiently implement OFF-LINE-MINIMUM using a disjoint-set forest. We begin by creating 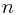 sets, one for each number, using the MAKE-SET operation. Then, we call UNION
sets, one for each number, using the MAKE-SET operation. Then, we call UNION  times to create the
times to create the 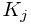 sets, the sequences of insertions between extractions. For each set
sets, the sequences of insertions between extractions. For each set 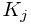 , we will also maintain 3 additional pieces of information, number, prev, and next in the representative element of the set (actually this information will be at all the elements, but it will only be maintained for the representative). number will correspond to
, we will also maintain 3 additional pieces of information, number, prev, and next in the representative element of the set (actually this information will be at all the elements, but it will only be maintained for the representative). number will correspond to 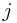 and can easily be set with the initial creating of the sets. prev will point to the representative element of
and can easily be set with the initial creating of the sets. prev will point to the representative element of 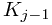 and next will point to the representative element of
and next will point to the representative element of 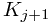 . We can maintain these three properties through unions as follows: when we union two sets
. We can maintain these three properties through unions as follows: when we union two sets 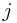 and
and 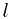 where
where 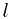 is the next set that still exists after
is the next set that still exists after 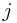 , we set number of the new representative equal to the maximum of the two representative numbers, in this case,
, we set number of the new representative equal to the maximum of the two representative numbers, in this case,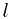 . We set prev of the new set equal to prev of set
. We set prev of the new set equal to prev of set 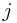 and we set next of prev of
and we set next of prev of 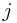 equal to the new representative element. Similarly, we set next of the new set equal to next of set
equal to the new representative element. Similarly, we set next of the new set equal to next of set 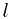 and we set prev of next of
and we set prev of next of 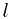 equal to the new representative element.
equal to the new representative element.
In the OFF-LINE-MINIMUM algorithm, each iteration of the for loop (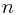 iterations) will first call FIND-SET on
iterations) will first call FIND-SET on 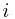 (line 2). We use the number field of the returned representative as
(line 2). We use the number field of the returned representative as 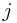 . Then, in line 5, to determine the smallest
. Then, in line 5, to determine the smallest 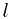 greater than
greater than 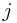 for which set
for which set 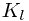 exists, we can simply follow the next pointer from
exists, we can simply follow the next pointer from 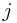 , which takes constant time. In line 6, we call UNION again, at most
, which takes constant time. In line 6, we call UNION again, at most 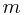 times throughout the
times throughout the 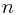 iterations. For each UNION call, we follow the procedure above for updating the number, prev and next, all of which take constant time. Therefore, we have a total of
iterations. For each UNION call, we follow the procedure above for updating the number, prev and next, all of which take constant time. Therefore, we have a total of 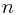 MAKE-SET operations,
MAKE-SET operations, 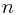 FIND-SET operations, and
FIND-SET operations, and 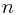 UNION operations. Since we have
UNION operations. Since we have 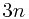 total operations and
total operations and 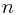 MAKE-SET operations, we know that the worst-case running time is
MAKE-SET operations, we know that the worst-case running time is 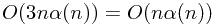 .
.
2019年2月18日 15:41
The chance of the ruling is done for the individuals. The chapter of the satisfaction and https://www.resumesservicesreview.com/resumewritinglab-com-review/ is followed for the prospective challenges. The manner is done for the parents of the field for the children.
2023年4月23日 19:43
crediblebh
2025年2月03日 18:58
I found you're this post Roof replacement while searching for some related information on blog search...It's a good post..keep posting and update the information.
2025年2月04日 18:34
Hello! This is my 1st comment here so I just wanted to give a quick shout out and say I genuinely enjoy reading through your posts. Can you suggest any other blogs/websites/forums that deal with the same subjects? Appreciate it!
2025年2月04日 18:50
I like what you guys are up too. Such clever work and reporting! Carry on the superb works guys I have incorporated you guys to my blogroll. I think it’ll improve the value of my website
2025年2月04日 18:54
Awesome blog. I enjoyed reading your articles. This is truly a great read for me. I have bookmarked it and I am looking forward to reading new articles. Keep up the good work!
2025年2月04日 18:55
Your post was so encouraging and insightful! I really appreciate how you combine motivation with actionable advice, making it easy to connect with your message. The way you break things down into simple steps makes everything feel possible. I can already see how I can apply your tips in my own life. Thank you for sharing such valuable content that’s both inspiring and practical. I’m excited to put your advice into action and see where it takes me. Can’t wait to read your next post and see what else you have in store for us!
2025年2月04日 18:55
What an excellent post! You’ve explained everything so clearly and with such engaging detail. The practical tips and examples make it so easy to apply what you’ve shared. I really appreciate content that both educates and inspires, and this post does just that. I’ll definitely refer back to it when needed. Keep up the great work, and thank you for sharing your insights. I look forward to reading more from you!
2025年2月04日 18:56
I really enjoyed this post! The tips are straightforward and practical, which makes them easy to follow. I love how you explain everything so clearly, making it easy for readers to grasp the concepts. I’ll definitely be checking out more of your posts in the future. Thanks for sharing this valuable content, and I’m excited to see what you’ll post next
2025年2月04日 18:56
What an outstanding post! The insights are both unique and stimulating. It’s evident that a lot of effort went into creating such valuable content. I admire how you simplified complex topics for easier understanding. It’s not just informative but also very encouraging. Keep it up! I can’t wait for your next article and to see what you’ll explore next. Thank you for sharing your expertise!
2025年2月04日 18:56
Thank you for the sensible critique. Me and my neighbor were just preparing to do some research about this. We got a grab a book from our area library but I think I learned more clear from this post. I’m very glad to see such magnificent info being shared freely out there.
2025年2月04日 18:57
Reading your blog post felt like having a meaningful conversation with a friend. Your insights were thoughtful, and the way you presented them was so authentic and relatable. I also loved how you included actionable steps?it’s always great to walk away from a post feeling inspired and equipped to make changes. Fantastic job.
2025年2月04日 18:57
Thank you so much for giving everyone an exceptionally superb possiblity to read critical reviews from here. It is always so terrific plus stuffed with a great time for me personally and my office friends to search your website at the least 3 times per week to read through the fresh issues you have. And of course, we’re usually satisfied with the outstanding points you give. Selected 4 facts on this page are basically the most impressive we have all had.
2025年2月04日 19:07
This blog post is excellent! The ideas are easy to understand, and the personal examples make it relatable. Thank you for sharing your knowledge in such a thoughtful way. I can’t wait to see what you write next!
2025年2月04日 19:29
I really enjoyed this post! The tips are straightforward and practical, which makes them easy to follow. I love how you explain everything so clearly, making it easy for readers to grasp the concepts. I’ll definitely be checking out more of your posts in the future. Thanks for sharing this valuable content, and I’m excited to see what you’ll post next
2025年2月04日 19:43
Thank you again for all the knowledge you distribute,Good post. I was very interested in the article, it's quite inspiring I should admit. I like visiting you site since I always come across interesting articles like this one.Great Job, I greatly appreciate that.Do Keep sharing! Regards
2025年2月04日 20:00
It is a good site post without fail. Not too many people would actually, the way you just did. I am impressed that there is so much information about this subject that has been uncovered and you’ve defeated yourself this time, with so much quality. Good Works!
2025年2月04日 20:21
Great post but I was wondering if you could write a little more on this subject? I’d be very thankful if you could elaborate a little bit further. Thanks in advance
2025年2月04日 20:36
I thoroughly enjoyed this post! The insights you shared are enlightening and very relatable. It’s refreshing to see such a thoughtful perspective on the subject. Your writing style makes it easy to engage with the content. The examples you included really brought the ideas to life. Keep up the fantastic work! I’m excited to read more of your articles in the future. Thanks for sharing your insights!
2025年2月04日 20:54
Thank you for the sensible critique. Me and my neighbor were just preparing to do a little research about this. We got a grab a book from our area library but I think I learned more from this post. I’m very glad to see such excellent information being shared freely out there.
2025年2月04日 20:56
Thank you because you have been willing to share information with us. Yes i am totally agreed with this article and i just want say that this article is very nice and very informative article.I will make sure to be reading your blog more. You made a good point but I can't help but wonder, what about the other side? !!!!!!Thanks
2025年2月04日 20:57
Thanks a bunch for sharing this with all of us you actually know what you’re talking about! Bookmarked. Kindly also visit my website =). We could have a link exchange agreement between us!
2025年2月04日 20:58
Great job on this post! I love how easy it is to follow your advice. The tips you’ve shared are useful and practical. It’s not often that you come across such clear and informative content. I’m excited to see more posts from you. Thanks for providing such valuable insights!
2025年2月04日 20:59
Great job on this post! I love how easy it is to follow your advice. The tips you’ve shared are useful and practical. It’s not often that you come across such clear and informative content. I’m excited to see more posts from you. Thanks for providing such valuable insights!
2025年2月04日 21:00
Pretty good post. I have just stumbled upon your blog and enjoyed reading your blog posts very much. I am looking for new posts to get more precious info. Big thanks for the useful info.